Hypothesis Testing
For this assignment, you will use the DOE experimental data
that your practical team have collected both for FULL Factorial and FRACTIONAL
Factorial.
DOE PRACTICAL TEAM MEMBERS (fill
this according to your DOE practical):
1. Serena (Iron man)
2. Trisyia (Thor)
3. Jun Xiang (Captain America)
4. Kai Rong (Black Widow)
5. Person E (Hulk)
6. Jerome (Hawkeye)
Data collected for FULL factorial design using
CATAPULT A (fill this according to your DOE practical result)
Data collected for FRACTIONAL factorial design using CATAPULT B (fill this according to your DOE practical result):
Iron Man will use Run #2 from FRACTIONAL factorial and Run#2
from FULL factorial.
Thor will use Run #3 from FRACTIONAL factorial and Run#3
from FULL factorial.
Captain America will use Run #5 from FRACTIONAL factorial and
Run#5 from FULL factorial.
Black Widow will use Run #8 from FRACTIONAL factorial and
Run#8 from FULL factorial.
Hulk will use Run #3 from FRACTIONAL factorial and Run#3
from FULL factorial.
Hawkeye will use Run #8 from FRACTIONAL factorial and Run#8
from FULL factorial.
USE
THIS TEMPLATE TABLE and fill all the blanks
|
The QUESTION |
The catapult (the ones that were used in the DOE practical)
manufacturer needs to determine the consistency of the products they have
manufactured. Therefore, they want to determine whether CATAPULT A produces
the same flying distance of projectile as that of CATAPULT B. |
|
Scope of the
test |
The human factor is
assumed to be negligible. Therefore, different user will not have any effect
on the flying distance of projectile.
Flying distance for
catapult A and catapult B is collected using the factors below: Arm length = 32.6cm Start angle = 20 degree Stop angle = 90 degree |
|
Step 1: State the
statistical Hypotheses: |
State the null hypothesis
(H0): At arm length of 32.6cm,
start angle of 20 degree and stop angle of 90 degree, using a different
catapult will not affect the flying distance. X = µ
State the alternative
hypothesis (H1): At arm length of 32.6cm,
start angle of 20 degree and stop angle of 90 degree, using a different
catapult will affect the flying distance X > µ |
|
Step 2: Formulate an
analysis plan. |
Sample size is 8 Therefore
t-test will be used.
Since the sign of H1
is >, a right tailed test is used.
Significance level (α) used in this test is 0.05
|
|
Step 3: Calculate the
test statistic |
State the mean and
standard deviation of sample catapult A: Mean = 83.5 Standard deviation = 3.15 State the mean and
standard deviation of sample catapult B: Mean = 80.9 Standard deviation = 3.31 Compute the value of the test statistic (t): n1
= 8 n2
= 8 s1 =
3.15 s2
= 3.31 X1 =
83.5 X2 =
80.9 |
|
Step 4: Make a
decision based on result |
Type of test (check one
only) 1. Left-tailed test: [ __
] Critical value tα = - ______ 2. Right-tailed test: [ 1.51 ] Critical value tα = 1.860 3. Two-tailed test: [ __ ] Critical value tα/2 = ± ______ Use the t-distribution
table to determine the critical value of tα or tα/2 Compare the values of test statistics, t,
and critical value(s), tα or ± tα/2
Therefore, Ho is accepted. |
|
Conclusion
that answer the initial question |
At arm length of 32.6cm,
start angle of 20 degree and stop angle of 90 degree, using a different
catapult will not affect the flying distance. |
|
Compare your
conclusion with the conclusion from the other team members. What
inferences can you make from these comparisons? |
Both Kai Rong
and my decision was the same in that the flying distance between both catapults
were the same. While the rest had the conclusion that the flying distance of both
catapults were different. The inference
made is that the catapults made are inconsistent because although me and Kai
Rong obtain the result of same flying
distance, majority of the results were deemed to be different flying distance
meaning the catapults were inconsistent to each other. |


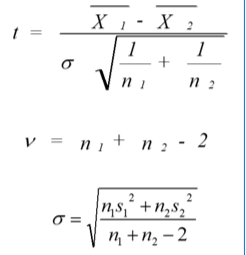


No comments:
Post a Comment